Hice la primera versión de mi juego Incremental Zoo hace doce años. La hice en inglés, porque el mundo de los incrementales, el género al que pertenece, existe en inglés. La posteé en Reddit, en una comunidad llamada precisamente “incremental games”, y me fue bastante bien. Mi pequeño zoológico se convirtió en un favorito, no de los principales, pero sí querido y recordado en el tiempo.
Con los años, aparecieron copias e imitaciones, algunas como apps para celulares. Ninguna hizo historia.
Hace unos meses lo quise retomar, para resolver algunas cuestiones que no estaban del todo bien en el original. Y descubrí que alguien ya lo había hecho por mí. Un estadounidense llamado Robert Munafo se había tomado el trabajo de corregir cosas y mejorar equilibrios, y tenía su propia versión a la vista.
Adopté su versión como nuevo punto de partida (nos escribimos un par de mails muy amables), hice unos pocos cambios más, y volví a postear el juego en la comunidad de Reddit.

Otra vez la respuesta fue encantadora. Apareció gente que lo recordaba de 2013. Conseguí unos cuantos likes y un montón de comentarios.
Ahí decidí traducirlo para mostrárselo, por fin, a mi propia gente, la de siempre, la que habla mi idioma. Después me dejé estar unos meses más, hasta que estos días me dije a mí mismo “¿qué estoy esperando?”, y acá estamos.
Un “juego incremental” suele ser algo bastante estático, con pocas imágenes o ninguna, donde no hay que reaccionar con rapidez a nada sino hacer que unos elementos produzcan otros, y los números crezcan todo lo posible. El origen, el juego que logró hacer de esto un subgénero, es Cookie Clicker (el link lleva al artículo en Wikipedia), que apareció en 2013 y me motivó a hacer Incremental Zoo.
En mi juego se trata de comprar animales y lograr que se reproduzcan en el zoológico. (Esto no sonaba tan incorrecto en 2013. Ahora oímos la palabra zoológico y se nos atraganta la nostalgia). Una vez que se tienen suficientes, hay que hacer que valgan más y venderlos al mejor precio posible, para así comprar animales más caros.
El juego va presentando progresivamente nuevas especies, cada una más costosa y más difícil de criar que la anterior. La idea es llegar a tenerlas todas, hasta la última. Ir descubriendo las sucesivas especies es parte del suspenso del juego.
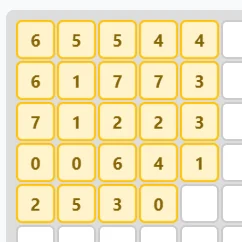
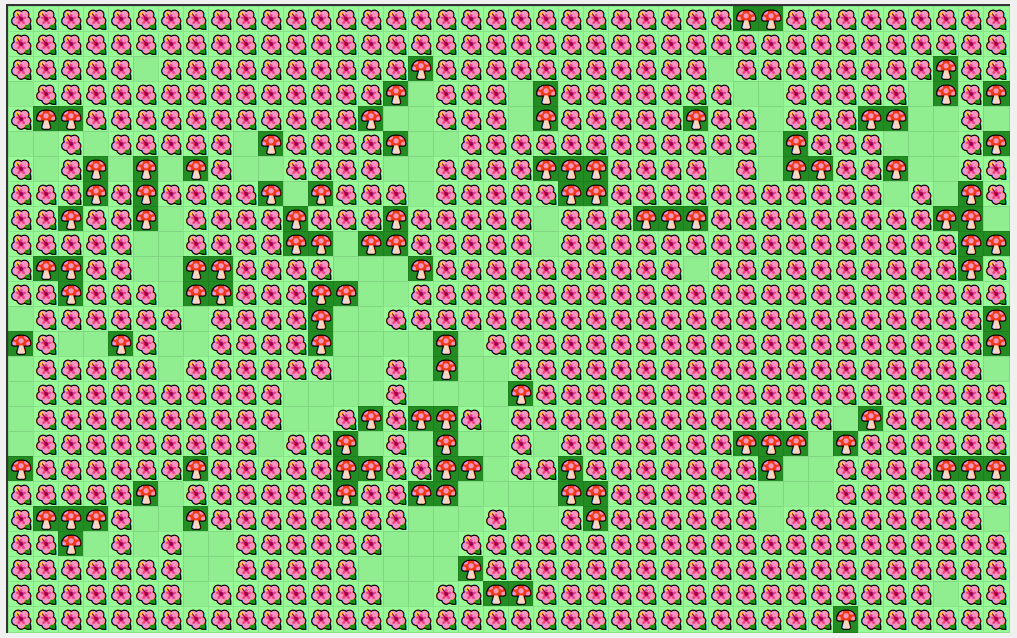
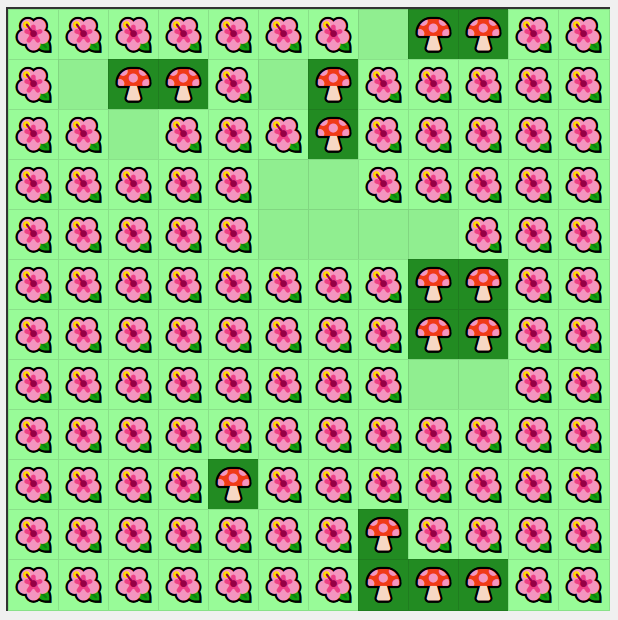
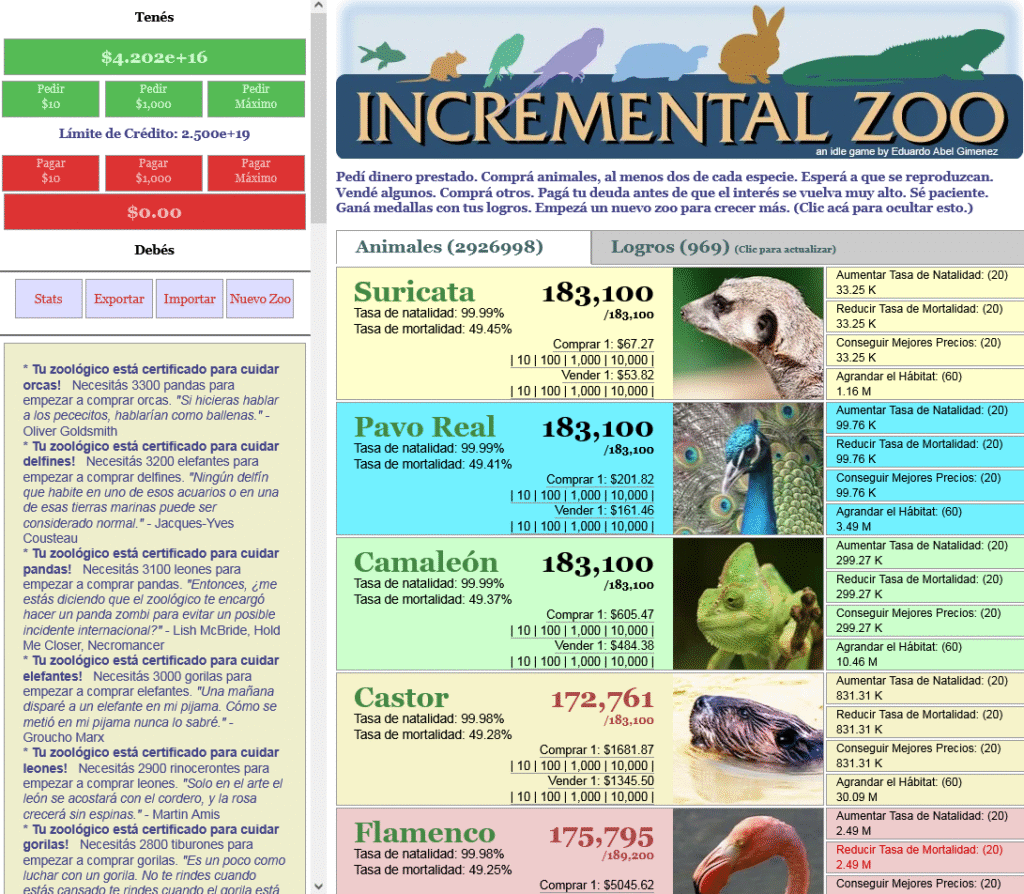
La imagen de arriba de todo muestra parte del juego en un estado avanzadísimo. El estado inicial es el que se ve a continuación:

La forma de empezar es pedir un crédito, clickeando el botón “Pedir Máximo”. Con los $50 que se obtienen, comprar 5 suricatas. Esperar a que se empiecen a reproducir. Cuando haya unos cuantos, vender algunos para mejorar la tasa de natalidad, reducir la tasa de mortalidad y mejorar los precios. Dato importantísimo: los animales tienen más probabilidades de reproducirse cuantos más ejemplares hay. (De hecho, a medida que avanzamos en el juego, cada nueva especie tiene menos probabilidades de reproducirse que la anterior, lo cual va aumentando el nivel de desafío).
En algún momento habrá que pensar en devolver el crédito inicial. O en pedir uno más grande, considerando que cuando llegues a tener la segunda especie (pavos reales), el límite de crédito aumentará, y así con cada especie que consigas.
Hay unos cuantos mecanismos más en el juego, pero la gracia está en ir descubriéndolos uno a uno. Este factor, el del descubrimiento, es esencial en la mayoría de los incrementales.
Hace doce años me hice fan de este tipo de juegos, y lo sigo siendo. Nunca dejé de jugar algún nuevo exponente del género. Y, de hecho, es prácticamente a lo único que me gusta jugar en la computadora o el teléfono. Algún día haré lo que tantas veces quise y nunca llegué a encarar: una guía básica de mis incrementales favoritos a lo largo del tiempo.
Mientras, te desafío a descubrir la última de las especies en Incremental Zoo. En el camino, tal vez le tomes el gusto a estos pasatiempos tan poco conocidos por acá.
Links: Incremental Zoo en castellano. Y, por si te interesa, Incremental Zoo en inglés.